Riemann vs Lebesgue (thank you Kia)

For decades now, I have wondered about the true difference between the Riemann and the Lebesgue integrals in analysis. The classical textbook explanation goes more or less like that: "Look, Riemann integrals are bad for commuting with taking the limit, let us try something else: if we subdivide the value space of the function instead of the interval of definition, everything turns well. So let us do it". I accepted this until some times ago. But then something happened.

Some insights from the mind of a know-it-all

I recently changed job. I like to have constructive conversations with my colleagues and I have worked hard at this in the last years. Unfortunately, I live with a heavy burden. There is a constant battle between the "know-it-all" (Kia) section of my brain and the Dr. Henry Jekyll part. She is continuously proposing to show how cool she happens to be and how much better would she run things and how it is possible that you don't see this and so on and so forth. In the course of time, Henry did indeed develop a strategy to cope with this: delayed gratification. He would not let Kia to start its rant immediately, but he generously would allow her a imaginary conversation with the culprit, impersonated by himself. There, Kia is allowed to use all the destructive rhetorics, cynicism, sarcasm and intellectual superiority she can muster. By the way, what does it matter that I changed job? It matters, since Kia get very very excited every time she does meet new persons, in particular in work. So I went through some hard times in the last months. Sometimes, however, Kia gives me insight.

If you are that good, explain me the difference between Riemann and Lebesgue integral

Impersonating a particularly nice and competent new colleague, short of nasty questions to throw at Kia, Henry just decided to resort to a random math question. By the way, note that my current job has nothing to do with academic maths, just to let you gauge the folly of my situation. Here he goes:

H: Well, if you are that good, give me the true difference between Riemann and Lebesgue integral.
K: How can you not know about this? I though you did know about math! Dear me, I will go through it, if this is really necessary.
H: Let me see...
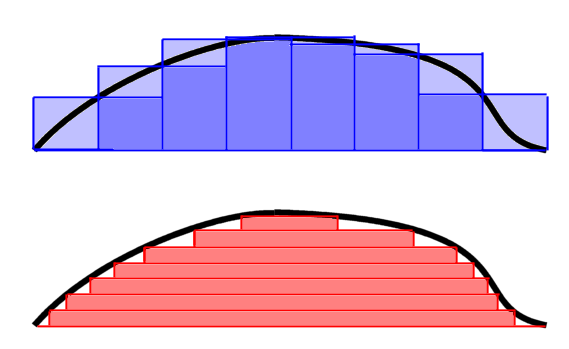
K: Every small child knows that in Riemann integral you partition the definition interval and in Lebesgue integral you partition the range of the values. Already in his doctoral thesis, which I happen to have read, my dear friend, in contrast to you ...
H: Hang on. Why now it should be better to partition the range of values?
K: Ah! You see? You did not learn anything in high school! You don't have any meaningful convergence theorems for Riemann integrals, so you have...
H: Why?
K: Why what?
H: Why you don't have any meaningful convergence theorems for Rimann integral and why it gets better with Lebesgue?

Yes, why?

Functions with bounded variation

There they stopped arguing: it became clear to them at once that they did not really knew why the world is that way. So they started a more intimate conversation in candlelight. The first thing what occurred to them is that by subdividing the interval of definition in equal intervals, I could not really control how much the the true integral of the function on a subinterval will differ from the area of the local approximation of the integral. This is bad. For doing this, in fact, they should make the intervals small when the function changes much and large when the function changes little.

And then I just had an image in my mind of the cover of Riesz functional analysis book, which I happened to be reading in the library of Tübingen university in 2004. They dug deeper, and brought up the fact that there I learned there about functions of bounded variation. Ah! Bounded variation! After 14 years, this small piece of information started to make sense. After 14 years, I understood why functions of bounded variations are so important. After 14 year, I finally discovered that they help controlling how a function changes in a interval and this is of crucial importance when defining the Riemann integral. As this would not be implicit in their very definition, to hell with them!

In fact, functions with bounded variations can be integrated very well in the sense of Riemann, I discovered. Incredibly also this obscure Riemann-Stieltjes integral makes sense suddenly!

But we want the convergence theorems. Go down some lines in Wikipedia: the space of functions with bounded variations form a Banach space in its own right, if endowed with an appropriate norm! Oh my God, why nobody told me that 14 years ago! We actually can have convergence theorems for Riemann integrals. So, why Lebesgue Kia, why Lebesgue?

The problem is, to make the space of functions with bounded variation to a Banach space, the required norm is given by the total variation of the function plus its Lebesgue norm!

So, in order to have converge theorems in the sense of Riemann, you must already know of Lesbegue integrals! Ah! I will not sleep this night because of this I know it...

Thank you Kia!